有偿编程，多元线性回归

谁用TB做过这个工作？请帮忙编程，提供报酬。微信：fzpkkk n个点,G(P1,C1）,G(P2，C2)...G(Pn,Cn),P是这个点距离当前k线的的k线数，P1<P2<...<Pn，C是价格。 求当前k线（P0=0)时的C0的值。 方法：用多元线性回归函数MLRS.先整理方程ax+res =b形式 构造系数矩阵和常数矩阵a b 然后带进去计算就行了 或者用其他方法也可以，只要能解决上面的问题就行。

price_n_a[4] = 87.67; bar_num_a[4] = 68; zcl_lsm(bar_num_a,price_n_a,Slope_n,Intercept_n); } OnBar(ArrayRef<Integer> indexs) { PlotString("CurrentBar",Text(CurrentBar) + ":" + text(h,2),h,Yellow); Commentary("斜率:" + text(Slope_n,1) + " 截距:" + text(Intercept_n)); zuiyoujie_n_se = Slope_n * CurrentBar + Intercept_n; PlotNumeric("线性规划",zuiyoujie_n_se,zuiyoujie_n_se,White); }

回复：老师真厉害

回复：这就是最简单的线性规划 啥时候搞出来 神经网络 机器学习 深度学习的算法 那才牛

DefsEvents OnInit() { SetArraySize(price_n_a, 5, 0); SetArraySize(bar_num_a, 5, 0); price_n_a[0] = 78.46; bar_num_a[0] = 191; price_n_a[1] = 72.88; bar_num_a[1] = 213; price_n_a[2] = 71.51; bar_num_a[2] = 224; price_n_a[3] = 84.52; bar_num_a[3] = 125;

//------------------------------------------------------------------------// 简称: testlsm// 名称: // 类别: 策略应用// 类型: 用户应用// 输出: Void//------------------------------------------------------------------------Params //此处添加参数Vars //此处添加变量 Series<Numeric> zuiyoujie_n_se; Array<Numeric> price_n_a; Array<Numeric> bar_num_a; Global Numeric Slope_n; Global Numeric Intercept_n;

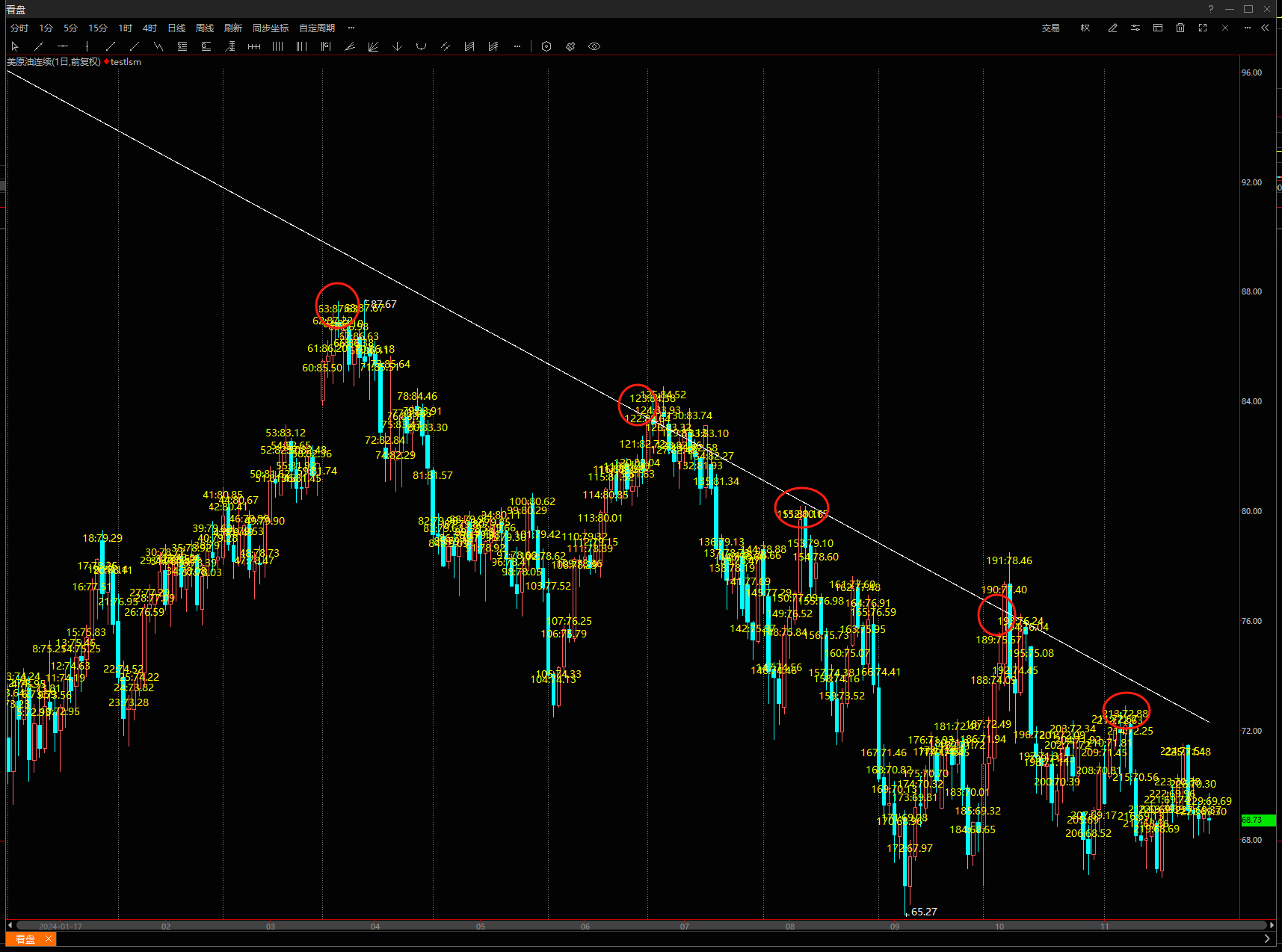输入图中画圆圈的5个点的数值，得出来的白色的拟合线，还算过关吧

//算出斜率 Slope_n_ref = (arrSize_n * sum_xy_n - sum_x_n * sum_y_n) /temp; //截距 Intercept_n_ref = (sum_y_n * sum_xx_n - sum_x_n * sum_xy_n) / temp; Return 1;End

Begin arrSize_n = GetArraySize(arr_X); if(arrSize_n<2) { Return 0; } sum_x_n = 0; sum_y_n = 0; sum_xy_n = 0; sum_xx_n = 0; Numeric i ; for i = 0 to arrSize_n - 1 { sum_x_n = sum_x_n + arr_X[i]; sum_y_n = sum_y_n + arr_Y[i]; sum_xx_n = sum_xx_n + arr_X[i] * arr_X[i]; sum_xy_n = sum_xy_n + arr_X[i] * arr_Y[i]; } temp = arrSize_n * sum_xx_n - sum_x_n * sum_x_n;

免费Params Arrayref<Numeric> arr_X; //数值型数组 Arrayref<Numeric> arr_Y; //数值型数组 NumericRef Slope_n_ref;//斜率 NumericRef Intercept_n_ref;//截距 Vars Numeric arrSize_n; Numeric sum_x_n(0); Numeric sum_y_n(0); Numeric sum_xx_n(0); Numeric sum_xy_n(0);

int main() { DataPoint dataPoints[] = {{1, 1}, {2, 2}, {3, 5}, {4, 4}, {5, 3}}; int numPoints = sizeof(dataPoints) / sizeof(dataPoints[0]); double slope = calculateSlope(dataPoints, numPoints); double intercept = calculateIntercept(dataPoints, numPoints, slope); printf("最佳拟合直线方程：y = %.2f * x + %.2f\n", slope, intercept); return 0;}

double calculateIntercept(DataPoint *points, int count, double slope) { double sumY = 0, sumXY = 0; for (int i = 0; i < count; i++) { sumY += points[i].y; sumXY += points[i].x * points[i].y; } double intercept = (sumY - slope * sumX) / count; return intercept;}

double calculateSlope(DataPoint *points, int count) { double sumX = 0, sumY = 0, sumXY = 0, sumXX = 0; for (int i = 0; i < count; i++) { sumX += points[i].x; sumY += points[i].y; sumXY += points[i].x * points[i].y; sumXX += points[i].x * points[i].x; } double slope = (count * sumXY - sumX * sumY) / (count * sumXX - sumX * sumX); return slope; }